Monotonieverhalten
Definition:
Eine Funktion ist monoton steigend, wenn ihre Ableitung stets größer oder gleich Null ist. (f'(x)≥0)
Eine Funktion ist streng monoton steigend, wenn ihre Ableitung stets größer Null ist. (f'(x)>0)
Analog für fallend:
Eine Funktion ist monoton fallend, wenn ihre Ableitung stets kleiner oder gleich Null ist. (f'(x)≤0)
Eine Funktion ist streng monoton fallend, wenn ihre Ableitung stets kleiner Null ist. (f'(x)<0)

An dem Graph dieser Funktion können wir zum Beispiel ganz einfach ablesen, dass die Funktion in (-∞,2.25) monoton fällt (nicht streng monoton, da f'(0)=0). Streng monoton fallend ist die Funktion jeweils in den Intervallen (-∞,0) und (0,2.25). Im Intervall (2.25,∞) steigt die Funktion streng monoton.


Beispiel:
Wir wollen das Monononieverhalten der folgenden Funktion bestimmen.

1. Funktion ableiten:

2. Nullstellen der Ableitung berechnen:

3. Intervalle einteilen:
Wir wissen dass die Funktion in den Intervallen zwischen unseren Nullstellen streng monoton ist. Wir wissen nur noch nicht ob fallend oder steigend.
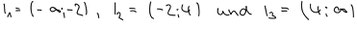
4. Stichproben einsetzen.
Um herauszufinden ob wir in den Intervallen nun streng monoton fallend oder steigend sind, müssen wir uns aus jedem Intervall eine beliebige Zahl nehmen und diese in die Ableitung einsetzten. Ist das Ergebnis positiv, so ist die Funktion in dem Intervall monoton steigend, ist das Ergebnis negativ, so ist die Funktion in dem Intervall monoton fallend.

